As my senior project in college, I worked on algorithms for Computer Go. A few weeks ago I talked about the UCT algorithm, the most popular algorithm as of late. UCT plays random games to explore the value of potential game tree paths. It converges to a reasonable answer much faster than normal Monte-Carlo searches.
My project ended up being about experimenting with playout policies. A playout policy is just a fancy way of saying, “How do you play a random game?”
If you play ten random games from a single position, you probably won’t get a very accurate average score. If you play 10,000 you still might not get an accurate score! This inaccuracy means that even though UCT is a good algorithm, it will take longer (since you need more random games) to converge to an acceptable answer. Garbage in, garbage out.
One of the current Computer Go champions, MoGo, was also one of the first to use UCT. Their paper improved random playouts by introducing “local shape features.” (Gelly et al). It looks for “interesting shapes” on the board, and leans towards playing those instead.
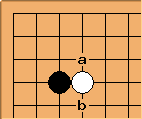
What’s an interesting shape? Take this position with black to move:
Ignoring the rest of the board, the position marked a is pretty much the only move for black. It is a strong move that effectively captures territory, attacks the white stone, and deprives it of a liberty. Position b is also potentially interesting for similar reasons.
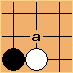
This kind of knowledge is really vague though. How can you make a quick test about whether something is interesting? MoGo decided to use hand-crafted information about 3×3 shapes. It takes every legal position on the board, and looks at the 8 stones around it. These form a pattern, and can be looked up in a pattern database. To see how this works, let’s take the two a and b positions from earlier, as if we were about to play at the center of a 3×3 area:
These are both patterns for the very favorable hane shape. Patterns are pretty flexible. You can introduce wildcards at intersections (which MoGo does). You can assign weights for a probability distribution. You can use neural networks to train them.
Patterns are also pretty fast as long as you stay under a 3×3 grid. Since the center is always empty, there are only eight stones to check. Of these eight, each intersection has four possibilities: Black, White, Empty, or Edge (edge of the board). That’s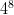 
, or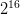 
possibilities. That means you can encode a pattern with just a 16-bit integer, and you can use that as an index into a 65,536-length array.
As an added bonus, patterns have identical symmetries. If you mirror or rotate a pattern, it is the same. If you flip the colors, you can also flip the score – meaning that you only need to store scores for one color. Combined with the fact that most patterns are not legal, there are under 2,000 unique 3×3 patterns. In fact, the two patterns above are identical.
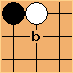
There are also patterns which are bad, and should probably be discouraged during normal play. For example, this pattern is the empty triangle, and you never want to play it:
Why are patterns useful, despite being local and having no knowledge about the board? They serve as an effective, quick local evaluation that is ideal for generating random games. A purely random game will have many bad moves. Pattern knowledge helps add some potentially good moves into the mix. MoGo claims to have gotten huge gains from their pattern knowledge.
For my project, I was tasked with trying out a few neural-network training algorithms for 3×3 patterns. The goal was to spit out a pattern database and compare the performance against other computer programs. I did all my work off an open-source project called libEGO.
Now, I love open source. I don’t love libEGO. It’s a messy project. The code is near-unreadable, there are almost no useful comments, the whitespacing is peculiar at best, bad at worst, and the formatting is atrocious. But it was small and had high coverage density, which made it ideal for experimentation.
I used a softmax function for choosing the next random move based on a pattern database. Every legal position on the board got a score of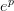 
, where 
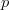is the value of the pattern at that position. The denominator of the probability is the sum of those scores for the entire board. The numerator is the score of a specific location on the board.
I tried a bunch of reinforcement learning functions from a recently published paper. Testing was a pain. Levente was kind enough to lend me access to a 100-node grid. I easily ate up every node for days on end. I hacked up Python scripts to battle-royale dozens of configurations against each other and spit out statistics. It was fun to see the results and analyze the games, but a single mistake could throw out a ton of time, since I’d have to recycle all the tests.
And I did make mistakes. With only 5-6 weeks of actual working time available, I had a few setbacks and I had to rush near the end. I didn’t end up with great results. On the other hand, I learned a lot, and I got to talk with one of the masters in the field every day. So in the end I really enjoyed the project, despite not being very good at AI.
I’m still fascinated by Go, and now UCT. I wrote some other UCT programs in between school ending and returning to Mozilla. One for Shogi, and one for m,n,k games (such as Connect 4 and Tic-Tac-Toe). The Shogi one didn’t do too well – I didn’t have enough domain knowledge to write a good evaluation function, and thus playouts were really slow. Connect 4 fared better, though my implementation would lose to perfect play. Tic-Tac-Toe played perfectly. twisty did an implementation as well and I believe managed to get perfect play on Connect 4.
Alas, I’m not sure if I’ll spend more time on it yet. My real calling is elsewhere.