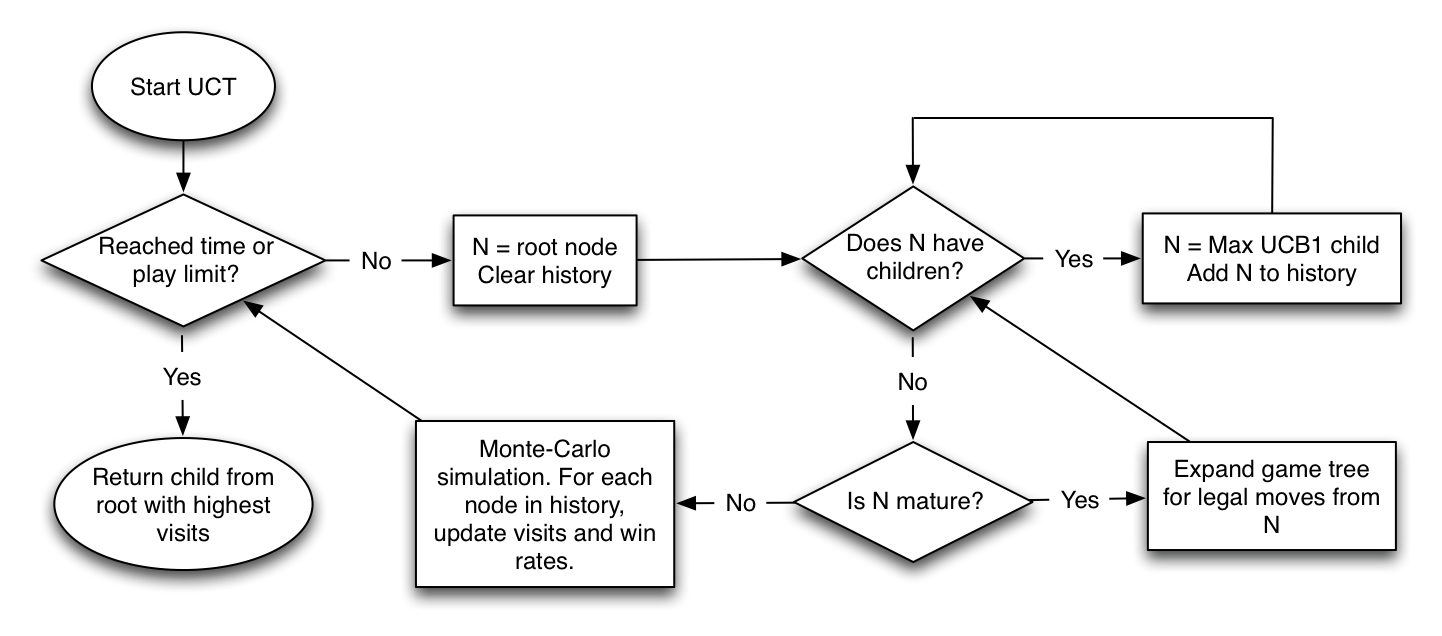
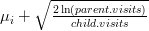While working on a project, I was wondering how to most efficiently implement string internalization. String “interning” is when two strings that compare true always have the same reference. This is quite nice as you can test if two strings are equal by just comparing their pointers.
It seems everyone uses hash tables for this, and indeed when I asked someone with more VM experience, he suggested using hash tables as well. I was still curious though, especially since SourceMod has a fancy-pants compressed “double-array” trie implementation. We knew that insertion time was poor, but I secretly hoped that this cost would be amortized over the much faster retrieval case.
I took a dump of ~5MB of plugin text from the forums and extracted all syntactically valid identifier tokens (including ones found in comments and strings). In total I had 553,640 strings, of which 19,852 were unique. This seems pretty reasonable as people tend to use similar names for identifiers. I set up four benchmarks:
- std::map<std::string, int> — Typical STL container (red-black tree I think)
- SourceMod::KTrie<int> — SourceMod’s Trie container
- SourceHook::THash<const char*, int> – SourceHook’s “TinyHash,” chained hash table
- SourceHook::THash<std::string, int> – Same, with more allocation involved
As a note, “TinyHash” is one of the first ADTs I tried to write, and it shows. Its stock find() function iterates over the whole table, instead of computing a hash, which is really slow. I filed a bug on this and hacked up my local copy to benchmark.
Each test gets run twice. The first “batch” run goes over all identifiers and inserts them if they are not already in the container. The second “retrieval” run does the same thing, except now there will be no string insertions since the table is populated.
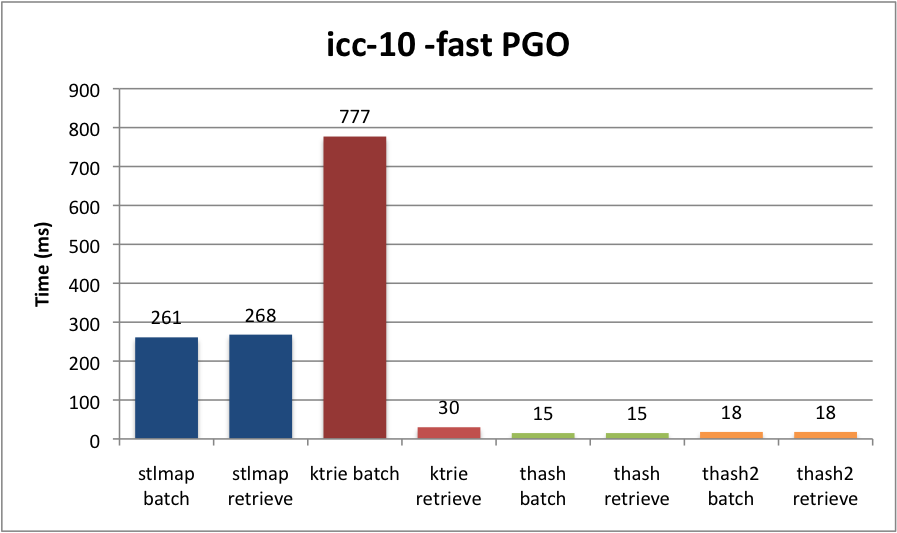
Here’s the results, in milliseconds. I used the Intel C++ Compiler, version 10, on my Macbook Pro (2.4GHz Core 2 Duo, 4GB RAM).
Whoa! Everyone was right. Well, I knew that insertion on our Trie was pants, but I was surprised to see that the cost was in no way amortized. In fact, it wasn’t even faster on retrieval! Why? I don’t know (yet), but if I had a guess, it’s because our Trie has to peek at memory a lot. David Gregg explained to me that the advantage of tries is sorting. He also theorized it might be faster on long strings, which is in line with my original benchmarks ages ago, where I used very long randomized strings. (Tries are also good for compression.)
Well, I has sad. Looks like we’ll be ditching KTrie for a chained hash table. At least for string interning. Someone is welcome to request a hash table ADT for SourceMod scripting as well.
I also benchmarked non-PGO ICC and non-PGO g++-4.2 if you would like to see other compilers.
Note 1: Go article returns next week.
Note 2: Firefox 3.5 comes out tomorrow (June 30th!)
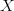 . You don’t know the true value of
. You don’t know the true value of 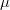 ).
).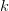 slot machines, each expressed as a random variable
slot machines, each expressed as a random variable 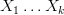 . Once again, you don’t know the true value of any
. Once again, you don’t know the true value of any 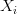 . How can you choose the right slot machine such that you minimize your losses? That is, you want to minimize the loss you incur from not always playing the most optimal machine.
. How can you choose the right slot machine such that you minimize your losses? That is, you want to minimize the loss you incur from not always playing the most optimal machine.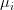 . You can then use this information to play on the observed best machine, but that might not end up being the most optimal strategy. You really need to balance exploration (discovering
. You can then use this information to play on the observed best machine, but that might not end up being the most optimal strategy. You really need to balance exploration (discovering